Rotational Motion

The laws and equations that govern nature and natural phenomena are described by physics. One prime focus of physics is the study of motion. We have dealt in detail about translational motion (objects that move along a straight or curved line) in the previous chapters, and now we will expand our view towards other types of motions as well.

We see rotational motion in almost everything around us. Every machine, all celestial bodies, most of the fun games in amusement parks and if you are a FIFA fan, and when you watch David Beckham’s familiar shot, the ball is actually executing rotational motion.

Objects turn about an axis. All the particles and the mass center do not undergo identical motions. All the particles of the body undergo identical motion. By definition, it becomes essential for us to explore how the different particles of a rigid body move when the body rotates.

Key Concepts in Rotational Motion

To understand rotational motion more clearly, we need to define some of its core concepts:

1. Angular Displacement

 Angular displacement measures the angle through which an object has rotated about a specific axis. It is similar to linear displacement in straight-line motion but involves rotation. The unit of angular displacement is typically measured in radians (rad), though degrees can also be used.

2. Angular Velocity

Angular velocity refers to the rate of change of angular displacement over time. It tells us how fast an object is rotating around its axis. Its unit is radians per second (rad/s). If the angular displacement increases rapidly over time, the angular velocity is high.

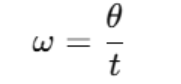
 Where:

• ω is angular velocity,
• θ is the angular displacement,
• t is the time.

3. Angular Acceleration

 Angular acceleration is the rate of change of angular velocity over time. Like linear acceleration, it can be positive (when the object speeds up) or negative (when it slows down). The unit for angular acceleration is radians per second squared (rad/s²).

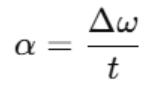
 Where:

• α is angular acceleration,
• Δω is the change in angular velocity,
• t is the time.

4. Moment of Inertia (I)

The moment of inertia is the rotational equivalent of mass in linear motion. It quantifies an object’s resistance to rotational acceleration. The greater the moment of inertia, the harder it is to rotate the object. The moment of inertia depends not only on the mass of the object but also on the distribution of the mass relative to the axis of rotation. The unit is kg·m².

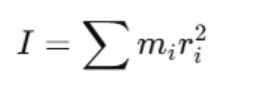
 Where:

• mi​ is the mass of the particle,
• ri​ is the distance from the axis of rotation.

5. Torque (τ)

 Torque is the rotational equivalent of force. It measures the tendency of a force to rotate an object about an axis. Torque depends on the force applied and the distance from the axis of rotation (the lever arm). The greater the torque, the greater the rotational effect.

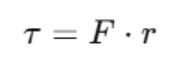
 Where:

• τ is torque,
• F is the applied force,
• r is the perpendicular distance from the axis of rotation.

Equations of Rotational Motion

Similar to the equations of linear motion (like v=u+atv = u + atv=u+at), rotational motion also follows its own set of equations that relate angular displacement, velocity, acceleration, and time:

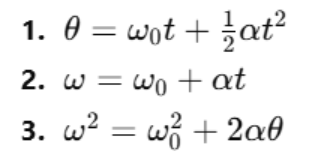
Where:

• θ is the angular displacement,
• ω0​ is the initial angular velocity,
• ω is the final angular velocity,
• α is the angular acceleration,
• t is time.

Conservation of Angular Momentum

Angular conservation is one of the greatest concepts in rotational motion. Similar to the linear momentum, angular momentum remains constant under the condition that there is no external torque of a system. This concept can be commonly seen in our daily lives, like when a figure skater closes his or her arms, so that he can turn quicker.

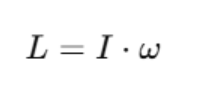
Where:

• L is angular momentum,
• I is moment of inertia,
• ω is angular velocity.

Applications of Rotational Motion  

Rotational movement plays a critical role in the study of the behavior of objects in other real life situations:

1. Wheels and Gears

Rotational motion is involved in the movement of wheels, pulleys and gears. Knowing about torque and angular velocity, engineers are able to create machines with little rotational energy consumption.

2. Earth’s Rotation

The ideal example of rotational motion is the rotation of the earth around its axis. This movement affects the day and night cycles and the movement of the ocean currents.

3.Sports

 In sports like figure skating or gymnastics, athletes use rotational motion to perform spins and flips. Understanding how to manipulate angular velocity and moment of inertia helps athletes control their movements.

4. Engineering

 Many devices such as motors, turbines, and flywheels are based on rotational motion. These devices convert energy from one form to another using the principles of angular velocity, acceleration, and torque.

Conclusion

Rotational motion is an important component of the mechanics of objects that surround us on a daily basis, such as cars or daily equipment. The principles of the subject such as angular displacement, velocity as well as torque are important in resolving problems in physics and engineering. Rotational motion laws are closely related to the laws of linear motion and usually adopt the same patterns, and they are used to understand physical systems in a more detailed manner.